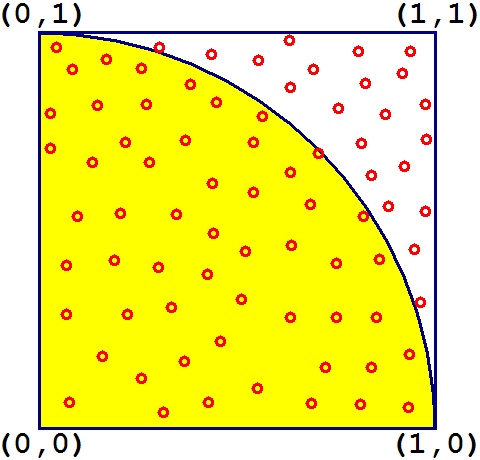
蒙地卡羅法(Monte Carlo Method)求圓周率的原理示意圖如下。正方形邊長為1單位長,面積為1平方單位;黃色扇形面積等於半徑為1單位長的1/4圓,面積為pi/4。在正方形內均勻隨機丟石頭,落在扇型內的機率 = 扇型面積÷正方形面積=pi/4。所以只要隨機產生N個座標(x,y),看看座標(x,y)落在扇形中(x2+y2<1)的次數有幾次。落在扇形中的次數除以N再乘上4的數值理論上就會接近圓周率PI。
程式中我們要不斷產生0<=x,y<1的座標點,使用frand()的方式來產生即可。完整程式碼如下。
 |
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
double throwPI(int N){
int i, count;
double x, y;
for( count = 0, i = 0; i < N; ++i ){
x = rand()/((double)RAND_MAX+1);
y = rand()/((double)RAND_MAX+1);
if( x*x + y*y < 1 ) ++count;
}
return 4.0 * count / N;
}
int main(void){
int i;
srand( time(NULL) );
for( i = 10; i <= 10000000; i *= 10 )
printf("%10d : %10.6lf\n", i, throwPI(i) );
}
|
下面是執行結果。理論上每次執行都會有點不同,但趨勢應該是相同的,也就是N愈大,得到的結果越接近PI。從數學上可以推估答案的收斂誤差為1/(2*Sqrt(N))。
 |
10 : 3.600000
100 : 3.240000
1000 : 3.176000
10000 : 3.131200
100000 : 3.138960
1000000 : 3.140680
10000000 : 3.141832
100000000 : 3.141683
|
第一次使用亂數就上手-目錄for C語言:
第一次使用亂數就上手 - 1. 即用篇for C
第一次使用亂數就上手 - 2. 基本篇for C
基本篇範例一:蒙地卡羅法(Monte Carlo Method)求圓周率
基本篇範例二:產生不重複樂透號碼
第一次使用亂數就上手 - 3. 推廣篇for C
產生常態分布亂數
RAND_MAX的試煉:原理x限制x修正
第一次使用亂數就上手 - 4. 原理篇for C
第一次使用亂數就上手 - 5. 基本篇for C
全站熱搜



 留言列表
留言列表