阿賢的部落格

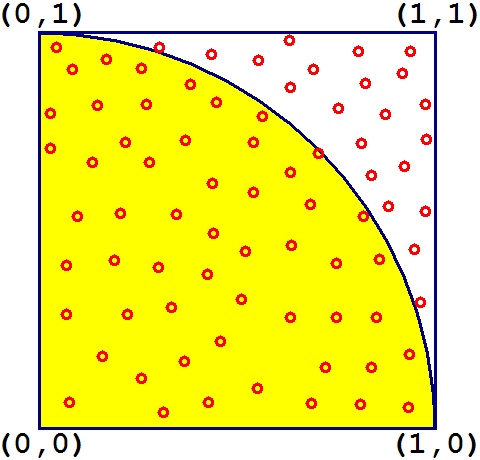
　　蒙地卡羅法(Monte Carlo Method)求圓周率的原理示意圖如下。正方形邊長為1單位長，面積為1平方單位；黃色扇形面積等於半徑為1單位長的1/4圓，面積為pi/4。在正方形內均勻隨機丟石頭，落在扇型內的機率 = 扇型面積÷正方形面積=pi/4。所以只要隨機產生N個座標(x,y)，看看座標(x,y)落在扇形中(x2+y2<1)的次數有幾次。落在扇形中的次數除以N再乘上4的數值理論上就會接近圓周率PI。

　　阿賢在上一篇裡簡單的介紹如何起始srand()及使用rand()函數，接下來要說說如何從基本函數rand()變化出最常使用的兩種「固定範圍均勻亂數」。
[1.] 產生 0.0 <= frand() < 1.0 的浮點數亂數( frand()為自訂函數 )
　　frand = rand()/((float)RAND_MAX+1)，或
　　frand = rand()/((double)RAND_MAX+1)

　　亂數的產生與使用對於電腦科學以及自然科學都有很重大的意義，20世紀初電腦的出生一部分的任務就是為了利用亂數計算出原子彈能不能爆炸。到了現代，統計學、電腦模擬、基因演算法等等先進的演算法仍然是建立在亂數上。最重要的，樂透電腦選號、網路遊戲掉寶、網路麻將洗牌、註冊認證碼等等現代虛擬世界常見的功能，也是用亂數做的！！所以，學會怎麼使用亂數是很重要的！
　　Fortran 90語言的標準中規定了標準亂數副程式RANDOM_SEED()以及RANDOM_NUMBER()，在F90以前的F77則沒有統一的標準。使用亂數前必須呼叫RANDOM_SEED()函式將亂數函數中的種子值(seed)初始化，不先呼叫本函數、或種子值固定，都會造成新手常見的「每次執行產生的亂數結果都相同」問題。大多數的Fortran compiler為了方便起見在使用者呼叫RANDOM_SEED()時會自動代入系統內的clock作為seed。GCC系列的Fortran則一定需要使用者自行設定seed值。一般而言，只需在程式開始使用亂數前呼叫一次RANDOM_SEED()即可，不必重複呼叫 (也不要不小心把RANDOM_SEED()包在迴圈裏面)。RANDOM_NUMBER(rand)是一個亂數副程式，使用時把要設為亂數的變數rand傳進去即可得到亂數，rand必須是浮點數型態。Fortran很特別的一點是，傳進去的參數rand可以是任意維度的陣列，所以可以一次得到大量的亂數。
　　在下面的程式中阿賢最簡單的示範如何使用RANDOM_SEED()、RANDOM_NUMBER()將亂數初始化，並印出來。如果是使用gfortran，則需要改成呼叫INIT_RANDOM_SEED()這個自訂的副程式(不是使用gfortran也可以用)。在INIT_RANDOM_SEED()內示範了如何使用SYSTEM_CLOCK()作為亂數seed的基礎。

　　亂數的產生與使用對於電腦科學以及自然科學都有很重大的意義，20世紀初電腦的出生一部分的任務就是為了利用亂數計算出原子彈能不能爆炸。到了現代，統計學、電腦模擬、基因演算法等等先進的演算法仍然是建立在亂數上。最重要的，樂透電腦選號、網路遊戲掉寶、網路麻將洗牌、註冊認證碼等等現代虛擬世界常見的功能，也是用亂數做的！！所以，學會怎麼使用亂數是很重要的！
　　C語言的標準中內建了亂數函數srand()以及rand()。使用亂數前必須呼叫 srand()函式將亂數函數中的種子值(seed)初始化，不先呼叫本函數、或種子值固定，都會造成新手常見的「每次執行產生的亂數結果都相同」問題。為了方便起見可以使用 time(NULL)這個系統內的時鐘作為seed，使每次執行產生的亂數序列不同。一般而言，只需在程式開始使用亂數前呼叫一次srand()即可，不必重複呼叫 (也不要不小心把srand包在迴圈裏面)。rand()是一個亂數函數，每呼叫一次rand()會傳出一個新的亂數。
　　在下面的程式中阿賢最簡單的示範如何使用srand、time將亂數初始化，並印出10次rand()亂數及RAND_MAX。

有些時候可能會需要讓程式暫停幾秒，可能是要等設備回應，也有可能，只是要讓CPU休息一下...在Fortran中如何做到這件事呢?
直覺上要讓程式暫停幾秒鐘可以利用讀時間 + do loop，下面阿賢利用SYSTEM_CLOCK這個Fortran90標準副程式以上述的概念實做出一個能讓程式暫停指定秒數的subroutine: sleep_secs。